휴대폰에서 전화번호 검색을 위해 상대방의 이름을 쳐서 검색한 적이 있으신가요?
이 때, 내부에는 효율적인 검색을 위해 HashTable 를 이용하여 전화번호를 찾습니다.
이 글에선 과연 HashTable는 무엇인지, 어떤 원리가 숨어있는 지를 알아보겠습니다.

참조: HashTable은 기본적인 DS로 다른 알고리즘이나 DS에 정말 많이 쓰입니다.

HashTable은 어떤 기능을 하나요?

어떤 값을 빠른 시간에 Search하거나 값을 Update를 할 수 있는 자료 구조입니다.
자세히 이야기하면, 키(key)를 통해 얻고자 하는 값에 접근 하는 자료구조입니다.

여러 기능 중 HashTable의 Search의 효율을 예와 함께 설명을 드리겠습니다.

문제 제시:

한 시골 학교에 6명의 학생이 있는 반과 그 반의 선생님이 있습니다.
어제 수학 시험을 쳤고 선생님은 각 학생의 수학 점수 기록을 가지고 있습니다.
이 중 ‘재석’이라는 학생이 자신의 수학점수가 궁금해서 선생님을 찾아 왔습니다.

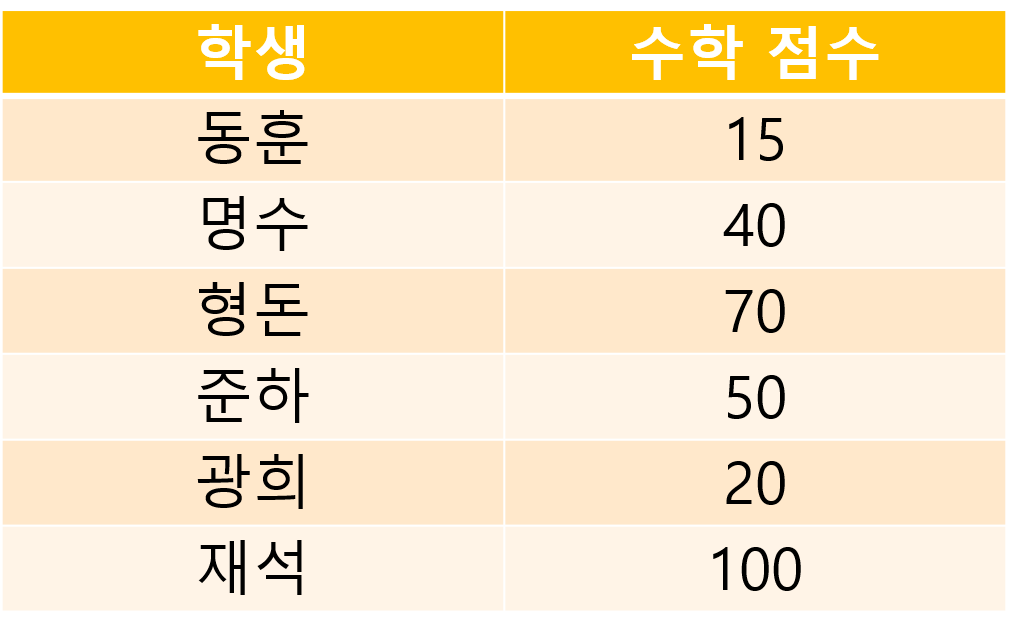
위는 수학점수 기록이고, 선생님은 어떻게 효율적으로 ‘재석’의 수학 점수를 알 수 있을까요?
※스스로 한 번 방법을 생각해봅시다!

Brute-force하게 해봅시다.

단순하게 위에서부터 학생의 이름을 한 명씩 비교해서 찾을 수 있습니다.
그 과정은 아래와 같습니다.

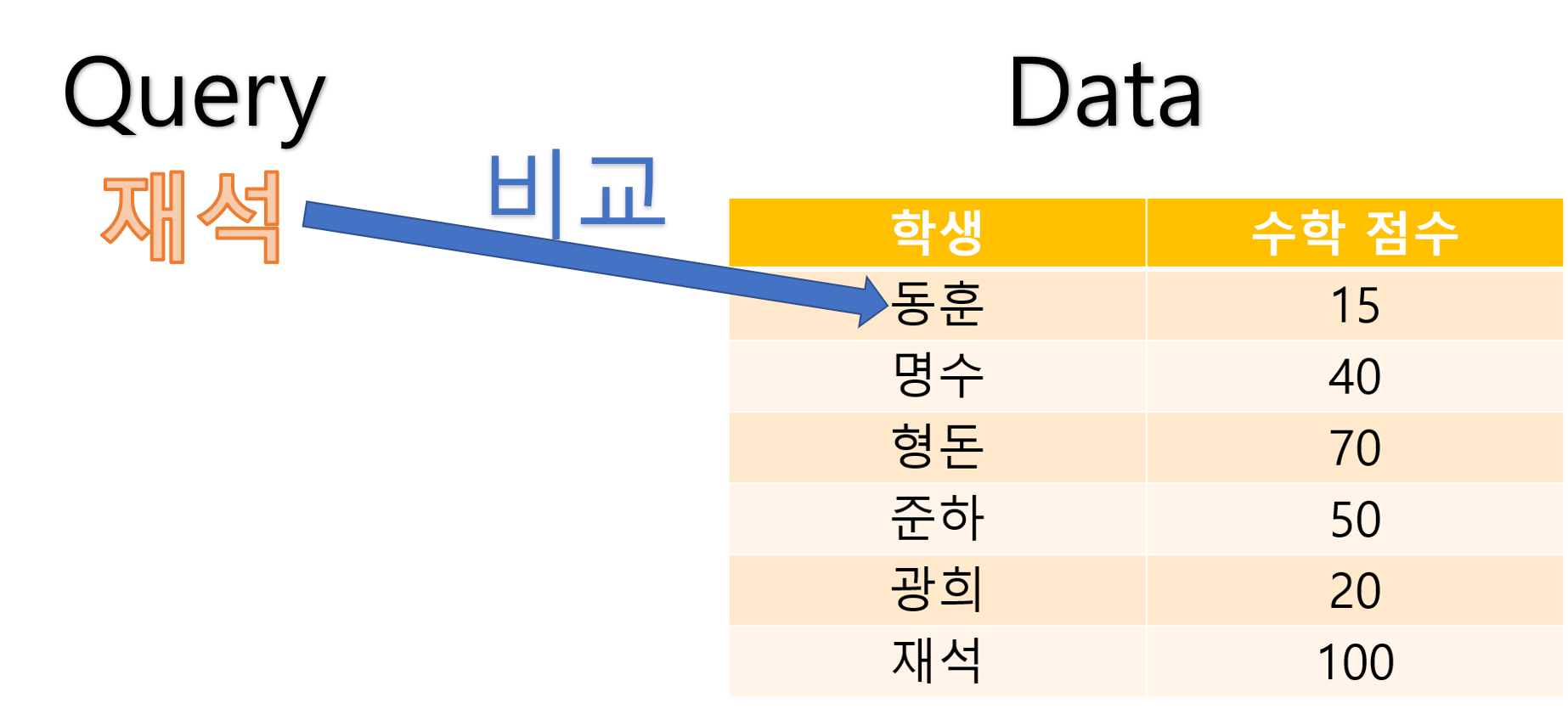
우리가 찾고 싶은 건 ‘재석’ 학생이지만 데이터의 첫 번째 칸은 ‘동훈’ 학생입니다.
따라서 다음으로 넘어갑니다.

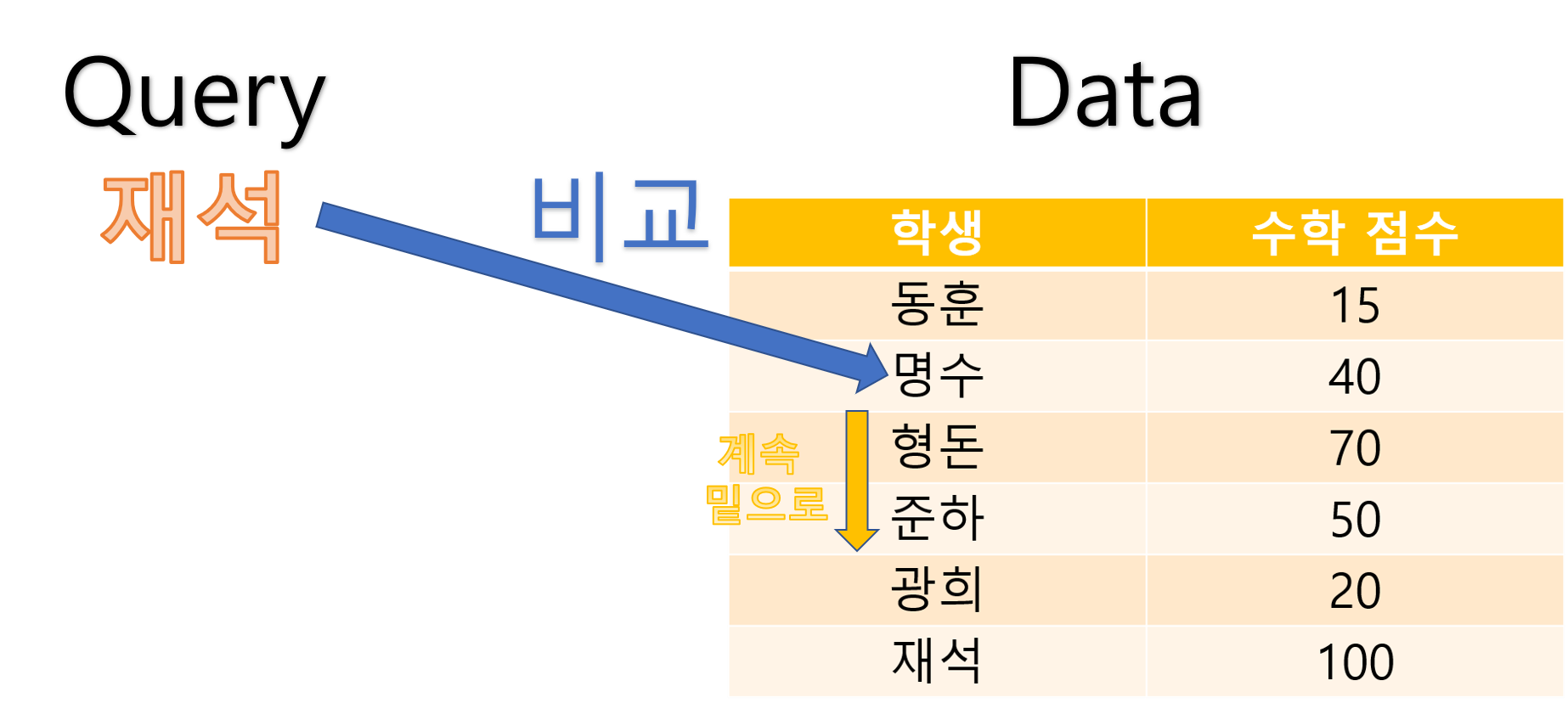
위의 경우에도 ‘재석’ 학생의 데이터가 아닙니다.
이처럼 이름이 찾는 이름이 아닐 경우에는 계속 다음 데이터로 넘어갑니다.

마지막에 비로소 재석의 이름에 해당하는 데이터를 찾았습니다.

하지만 위 방법으로 진행했을 경우, 최악의 경우 처음부터 모든 데이터를 검사해야 합니다.
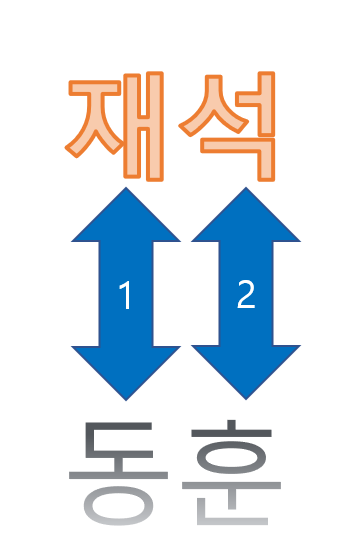심지어 왼쪽처럼 이름을 비교하는 상황에도 시간 cost가 발생합니다.

찾는 과정은 Time-complexity를 보았을 때, 최악의 경우는 O(N*M)입니다.
(이 때 N = 학생 수, M = 학생 이름의 길이)

더 나아가, ‘재석’ 뿐 아니라 다른 학생들도 수학 점수가 궁금해서 찾아오면 어떡할까요?
매 학생이 물을 때마다, 모든 데이터를 체크해야 하고, 이건 굉장히 비효율적입니다.
만약 K명의 학생이 물어본다고 가정하면 시간 소모는 O(N*M *K)가 됩니다.

따라서 물어보는 학생이 많으면 많을 수록 소모되는 시간은 기하급수적으로 커집니다.
이 비효율성을 줄이고자, 다음과 같은 HashTable이라는 자료구조가 고안되었습니다.

HashTable:

이 문제를 해결하는 아이디어는 Hashing와 Dynamic-array의 마법을 이용하는 것입니다.
사실, 이 두 가지의 비밀 뒤에는 수학, 통계, LUT 등 여러가지 고려할 것이 많습니다.
하지만, 이 글에서는 HashTable의 전체적인 구조에 관해서만 간단히 알아보겠습니다.

-참조 Dynamic-array의 마법을 알고 싶으면 Dynamic-array
-참조 Hashing의 마법을 알고 싶으면 Hashing

전체적인 구조:
※ 쉬운 이해를 위해, 몇 개의 전제 조건을 설정하겠습니다.

10개 slots의 slots-list로 시작
사용자 임의의 한글-LUT(lookupTable)
사용자 임의의 String-Hash 함수
Birthday-Paradox는 신경 쓰지 않음
잘못된 Hashing 함수로 인한 Duplicate-key는 신경 쓰지 않음

초기의 HashTable:

위는 아직 아무런 Key와 데이터가 없는 초기의 HashTable을 만든 모습입니다.
HashTable은 Keys - Hash - slots의 구조로 이루어져 있다고 생각하면 됩니다.
slots은 초기 사이즈가 10인 Dynamic-array로 되어있습니다.
Hashing 함수는 다음과 같은 두 단계로 이루어져있습니다.

String의 각 글자의 값을 합칩니다.
합친 값을 slots의 갯수로 %(Modulo)를 합니다.

Key를 받으면, Hashing이 Key를 Slots의 알맞은 index의 값으로 바꾸어 줍니다.
오른쪽은 임의의 한글-LUT로 Hashing의 값을 구할 때 도와줍니다.

HashTable 데이터를 넣는 과정:

아래는 ‘동훈’의 데이터를 넣는 과정입니다.

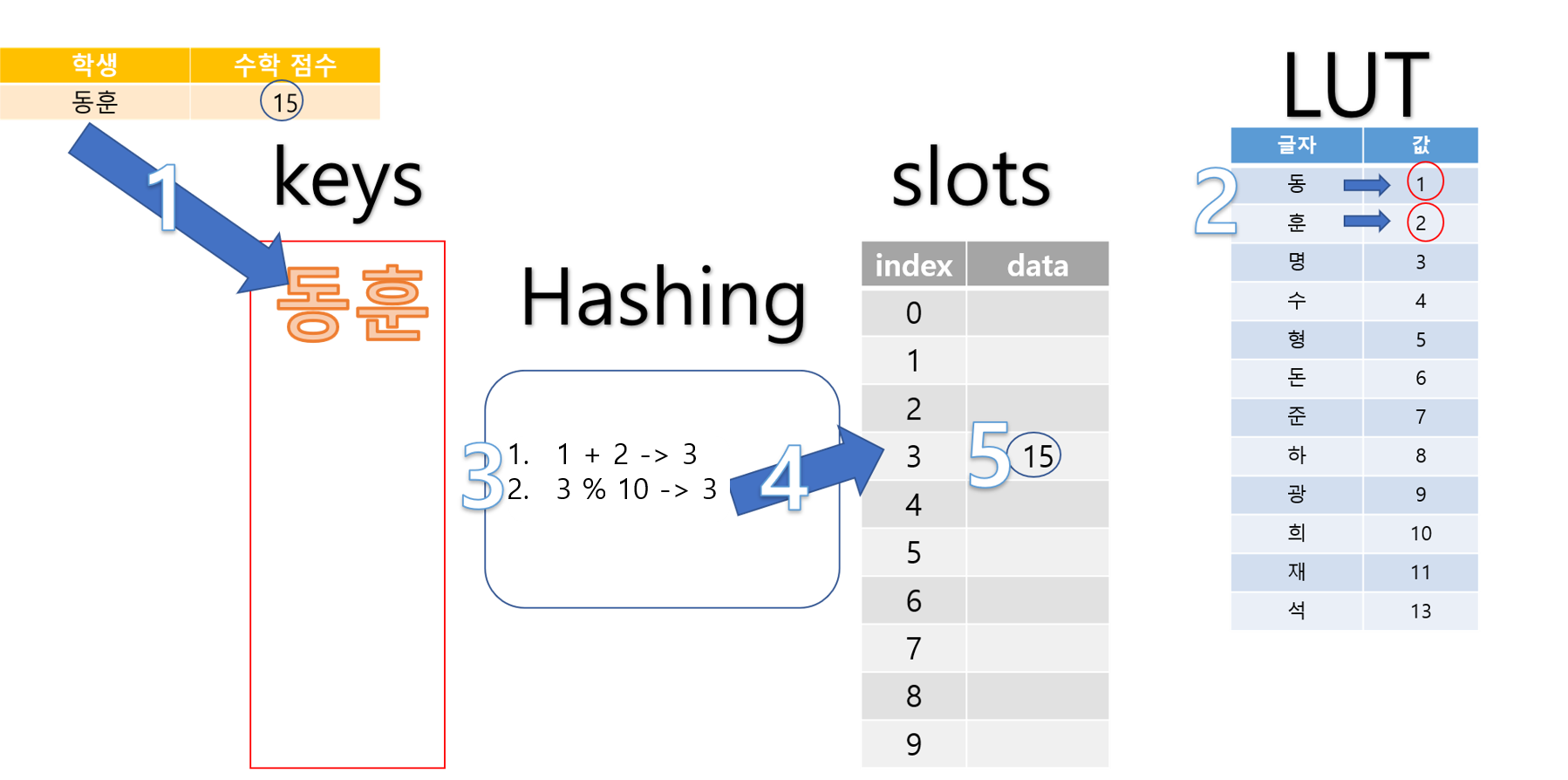
데이터를 넣는 과정은 크게 5단계로 이루어 집니다.

‘동훈’ 학생의 이름이 Key로 들어갑니다.
‘동훈’ 각각 ‘동’, ‘훈’에 해당하는 Decimal 값을 LUT에서 찾습니다.
LUT에서 찾은 값을 이용해 Hash-function에서 두 가지 단계로 처리합니다.
나온 값 3에 해당하는 Index를 가진 slot에 접근합니다.
해당하는 index의 slot에 ‘동훈’의 점수인 15를 넣습니다.

아래는 ‘명수’의 데이터를 넣는 과정입니다.

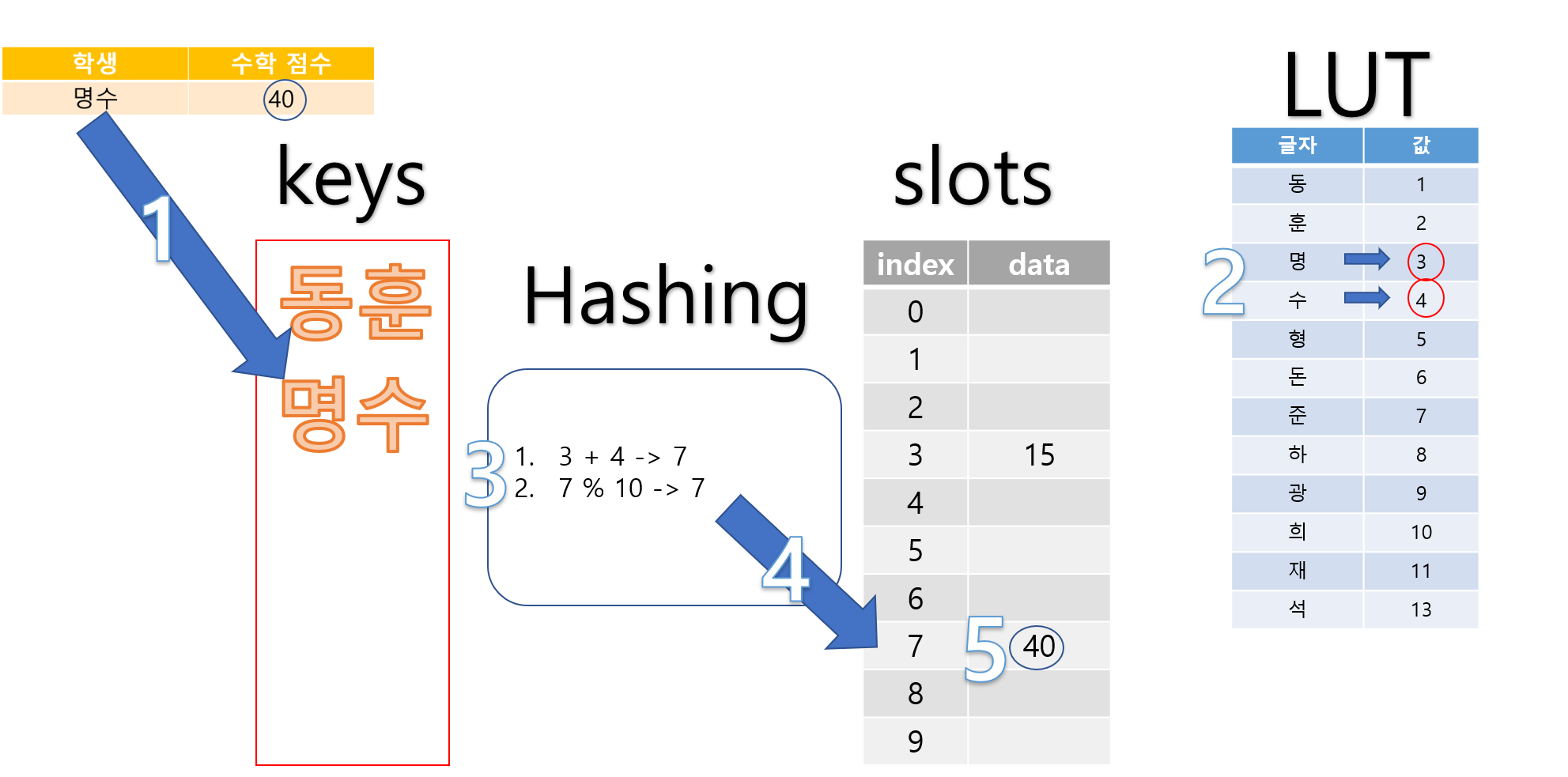
HashTable에 데이터를 다 넣은 상태:

아래는 모든 학생의 데이터를 다 넣고 난 후 HashTable의 모습입니다.

HashTable 데이터를 찾는 과정:

아래는 ‘재석’ 학생의 데이터를 찾는 과정입니다.

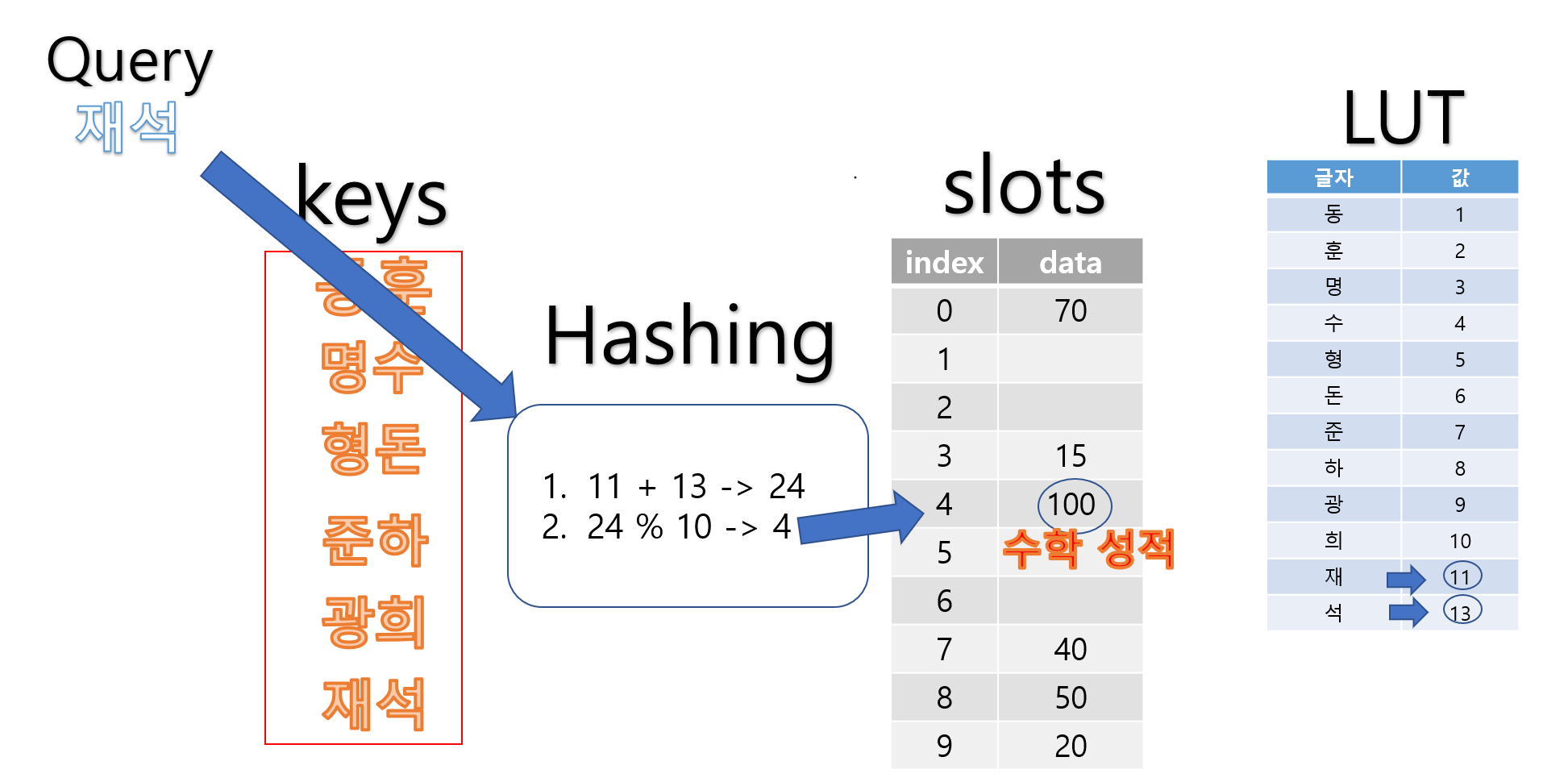
데이터를 찾는 과정은 데이터를 넣을 때의 과정과 비슷합니다.

Hash-func을 통해서 ‘재석’의 Index 값인 4를 찾는다.
index가 4인 slot에 접근한다.
index가 4인 slot에 저장된 데이터인 ‘100’을 도출한다.

아래는 Keys에 없는 ‘홍철’ 학생의 데이터를 찾는 과정입니다.

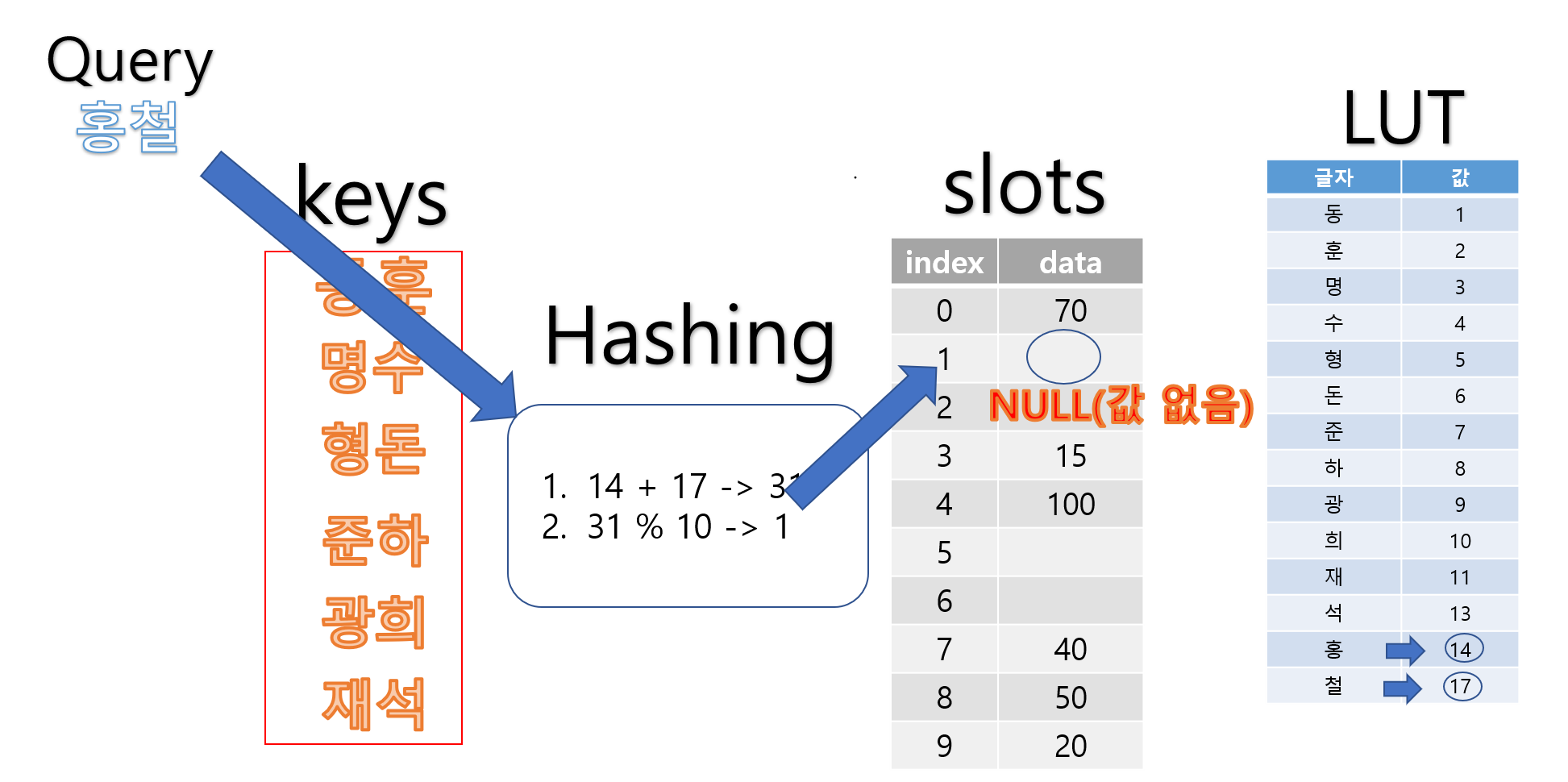
만약 기존의 키에 없었던 ‘홍철’이라는 학생 데이터를 찾으려고 하면
위처럼 Hash-func에 의해 index가 1인 slots에 접근하게됩니다.
하지만, index가 1인 slot에는 데이터가 없고 따라서 Null을 Return 합니다.

실제론, Birthday-paradox 같은 문제로 Collision이란 것이 생깁니다.
대처하기 위한 전략으론 Open-address나 separate-channing 등 몇 가지가 있습니다.
더 자세히 알아보기

HashTable의 평가:

일단 data를 Insert할 떄는 brute-force 방법보다 더 걸릴 수 밖에 없습니다.
각 데이터는 Hashing을 거쳐 저장되기 때문에 Hashing 하는 시간만큼 더 걸리는 것이죠.

Big-O notation으로 따지면, O(N*M)의 시간이 걸립니다.
(이 때, N = 넣고자 하는 학생 수, M = 각 학생의 이름 길이)
넣을 때의 시점에선 이전 방법보다 효율성이 좋다고는 하기 어려울 거 같습니다.

하지만, 물어보는 학생의 경우, 즉 쿼리를 처리할 때는 이전보다 훨씬 좋습니다.
이전에는 매번 가지고 있던 모든 데이터를 체크해야 했지만 이번에는 그렇지 않습니다.
각 학생은 자신의 이름을 Hash-func에만 넣기만 하면 바로 Index를 얻을 수 있습니다.
이 때 얻은 Index의 slot은 Dynamic-array의 마법으로 바로 접근할 수 있습니다.

Big-O notation으로 보면, O(K*M)의 시간이 걸립니다.
(이 때, K = Query의 수, M = 각 Query 학생의 이름 길이)
이 시간이 걸리는 이유는 각 Query들은 Hash-func 과정을 해야하기 때문에 어쩔 수 없이
Hashing에 걸리는 시간인 O(M)을 소모할 수 밖에 없습니다. 하지만 Search하는 시간은
O(1)으로 Linear하게 바로 원하는 값에 접근할 수 있습니다.
따라서, 이전보다 훨씬 좋은 Query 처리 속도를 가진다고 할 수 있습니다.

HashTable과 관련된 용어:

구현 언어에 따라 또는 구현 방법에 따라 또는 잠깐 언급한 Collision 전략에 따라
관련 용어들은 조금씩 다릅니다. 자주 쓰이는 것들로 HashMap, Map, Dictionary가 있습니다.
하지만 핵심은 Key-Value로 pair이 된 Collection이라는 것에서 같습니다.

참고로, Python에서는 Dictionary, Set이 대표적인 HashTable로 구현된 DataType입니다.

Python에서는 Set이 Value가 Binary인 HashTable로 되어있습니다.

실제 구현 by Python

구현 아이디어:

Dynamic-array
Hash

Code:

import os
import sys

# 한글-LUT
LUT = {'동': 1, '훈': 2, '명': 3, '수': 4
        '형': 5, '돈': 6, '준': 7, '하': 8
        '광': 9, '희': 10, '재': 11, '석': 13
        '홍': 14, '철': 17}

class HashTable:

  def __init__(self):
    self.Num_of_Slots = 10
    self.slots = [None]*10 # dynamic array

  # Hash-fun
  def _hash(self, name):
      global LUT
      index = 0
      #proc-1
      for chr in name:
        index += LUT[chr]
      #proc-2
      index %= self.Num_of_Slots

      return index

  def insert(self, name, data):
    index = self._hash(name)
    self.slots[index] = data

  def search(self, name):
    index = self._hash(name)
    value = self.slots[index]

    if value: # if it is not None
      return value
    else:
      return None