출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges

핵심개념

1.기본적인 modular arithmetic
2.DP(dynamic programming)

팁

먼저, 답의 정확성에서 문제가 발생하시면 Modular arithmetic에서 실수가 없었는지 체크바랍니다.
여기서 필요한 Modular arithmetic은 A%m = (B%m + C%m)%m 단, m = 20170805 입니다.

두 번째로, DP의 아이디어가 중요합니다.
이 문제는 2 * (m+1) * (n+1) 크기의 DP가 문제 풀기에 용이합니다.
각각 +1을 하는 이유는 i == m-1 이나 j == n-1의 경우를 계산할 때 편하게 하기 위함입니다.

DP에는 (a, b)의 형태로 a: 이전에서 가로 방향으로 온 경우 b: 이전에서 세로 방향으로 온 경우
로 나누시고 CityMap을 값을 체크하시면서 DP 값들을 처리하시면 됩니다.

그림 설명

각 DP의 값에는 이전에서 가로방향으로 들어온 경우와 세로 방향 들어온 경우로 나눕니다.

CityMap이 0인 경우

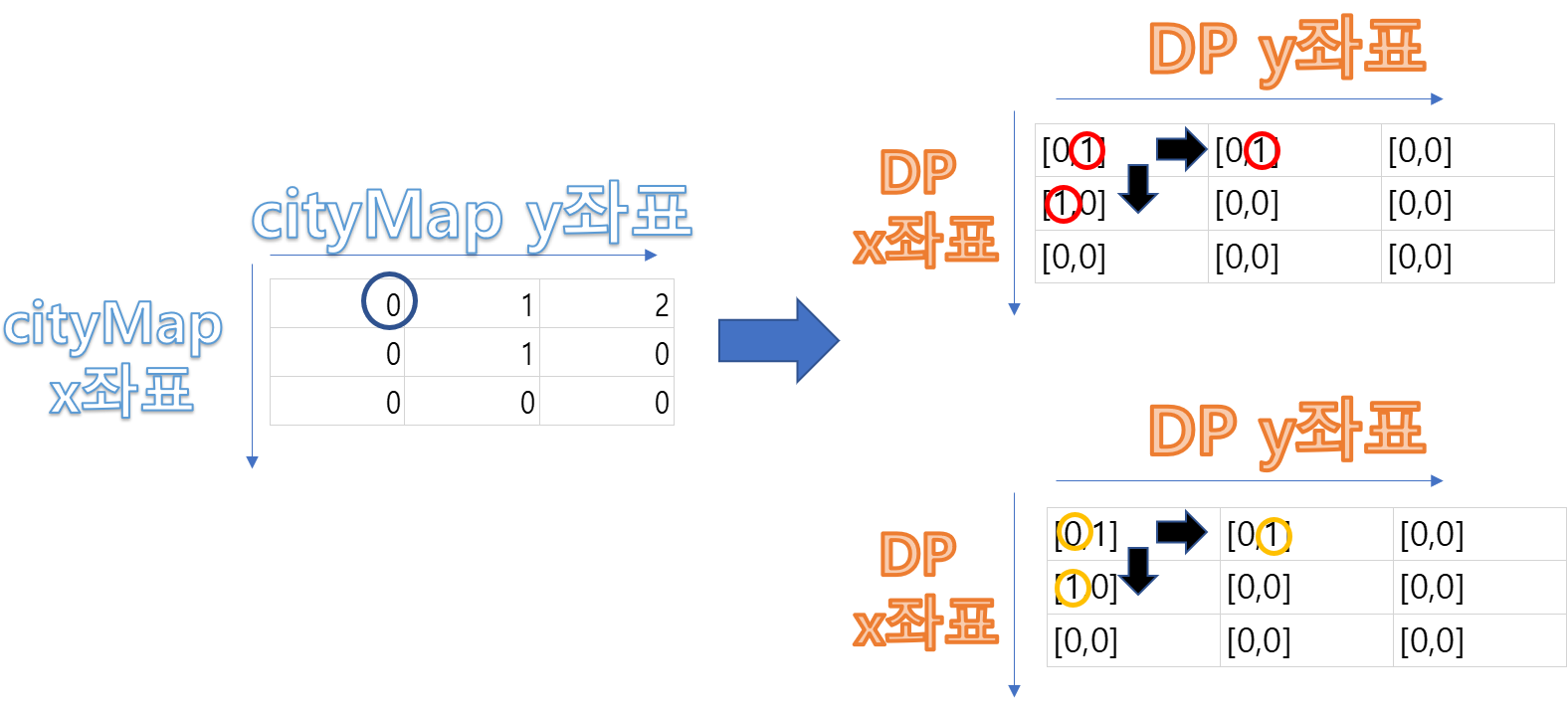
1. 어떤 방향이든 상관없이 dp[1][i][j+1]으로 저장
2. 어떤 방향이든 상관없이 dp[0][i+1][j]로 저장

CityMap이 2인 경우

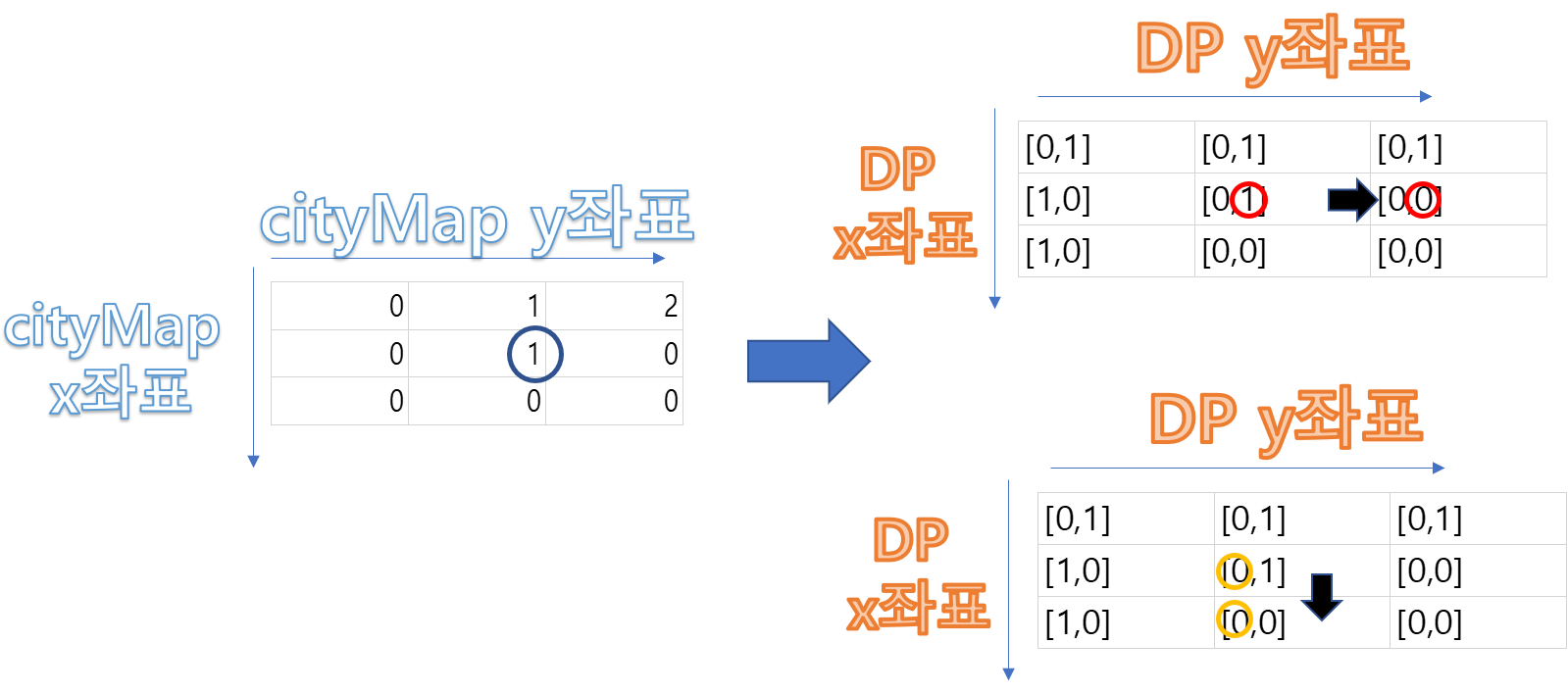※그림에 DP값을 1로 잘못 적었습니다. 1->2로 생각하시고 봐주세요.

1. Vertical하게 들어온 값은 오른쪽으로 dp[1][i][j+1]으로 저장
2. Horizontal하게 들어온 값은 밑으로 dp[0][i+1][j]으로 저장

CityMap이 1인 경우

그냥 CONTINUE

시간 효율성

O(m * n * 2)

Code:

import java.util.*;

class Solution {
  static final int MOD = 20170805;
  public static int solution(int m, int n, int[][] cityMap) {
    int[][][] dp = new int[2][m + 1][n + 1];
    dp[0][0][0] = 1;

    for (int i = 0; i < m; i++) {
      for (int j = 0; j < n; j++) {
        if (cityMap[i][j] == 0) {
          dp[0][i + 1][j] = (dp[0][i + 1][j] + dp[0][i][j] + dp[1][i][j]) % MOD;
          dp[1][i][j + 1] = (dp[1][i][j + 1] + dp[0][i][j] + dp[1][i][j]) % MOD;
        } else if (cityMap[i][j] == 2) {
          dp[0][i + 1][j] = (dp[0][i + 1][j] + dp[0][i][j]) % MOD;
          dp[1][i][j + 1] = (dp[1][i][j + 1] + dp[1][i][j]) % MOD;
        } else {
          ;
        }
      }
    }

    return (dp[0][m - 1][n - 1] + dp[1][m - 1][n - 1]) % MOD;
  }

  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int m = Integer.parseInt(sc.nextLine());
    int n = Integer.parseInt(sc.nextLine());

    int[][] cityMap = new int[m][n];
    String line = sc.nextLine();
    String[] lines = line.substring(1, line.length() - 1).split("\\],\\[");

    for (int i = 0; i < m; i++) {
      String[] newLine = lines[i].split(", ");
      for (int j = 0; j < n; j++) {
        cityMap[i][j] = Integer.parseInt(newLine[j]);
      }
    }
    System.out.println(solution(m, n, cityMap));
  }
}