우리가 군대의 점호시간에 현재 부대원을 보고함으로서, 현재 상태를 나타내듯이
프로그램을 구현 하는 과정 중, 많은 부분에서 현재 상태를 체크하고 보고하는 일이
많습니다. Bit를 이용한 BitMask로 상태를 표시하면 효율적일 때가 많습니다.
이 글에서는 BitMask가 무엇인지? 어떻게 쓰이는 지에 대해서 알아보겠습니다.
Bit의 마법:
많은 분들이 이미 아는 것처럼, 컴퓨터는 모든 것이 이진법으로 이루어져 있습니다.
10(decimal) = 1010(bin), 4(decimal) = 10(bin), 13(decimal) = 1101(bin)처럼
숫자의 경우, 컴퓨터는 우리의 십진법 숫자를 이진법 숫자로 바꾸어 해석합니다.
위 같은 사실은 우리가 “오호 2진법이군!”만 하고 넘어갈 것이 아니라
우리의 알고리즘에도 이 Bit성질을 적용할 수 있고 실제 구현에서도 자주 이용합니다.
BitMask란 ‘bit를 이용해 우리의 얼굴(mask)처럼 현재 상태를 표현한다.‘로 이해하면 됩니다.
아래에서는 이 bit 성질을 이용한 BitMask의 기능에 대해서 알아보겠습니다.
ALU의 회로나 CPU구조를 아신다면 더 깊은 이해가 됩니다.
어떤 기능을 할 수 있는가?
BitMask는 현재 상태를 표현, 변형 또는 비교 등의 기능을 수행 할 수 있습니다.
이 상태를 변형하거나 비교는 Bitwise함수를 이용하게 되는 경우가 많습니다.
Bitwise함수를 이용하는 이유는 이 함수들은 ALU 안의 OR 또는 AND Gate 등을 활용해
각 bit 단위 연산을 CPU에서 한 번에 계산하여, 효율성을 훨씬 높일 수 있기 때문입니다.
BitMask의 기능들은 아래의 문제와 함께 설명을 하겠습니다.
문제 제시
한 반에 학생 세 명이 있습니다. 어느 날 이 반에서 깜짝 조별 시험을 치기로 하였습니다.
시험에서 요구하는 건 ‘국영수사과’ 로 5개 과목이고, 오픈북 시험을 치기로 하였습니다.
시험은 쉬워서, 교과서만 있다면 학생은 과목에 해당되는 문제는 다 맞을 수 있습니다.
하지만 어떤 과목에 해당되는 교과서가 없다면 학생은 틀리게 될 것 입니다.
최대 두 명까지 조를 짤수 있습니다.
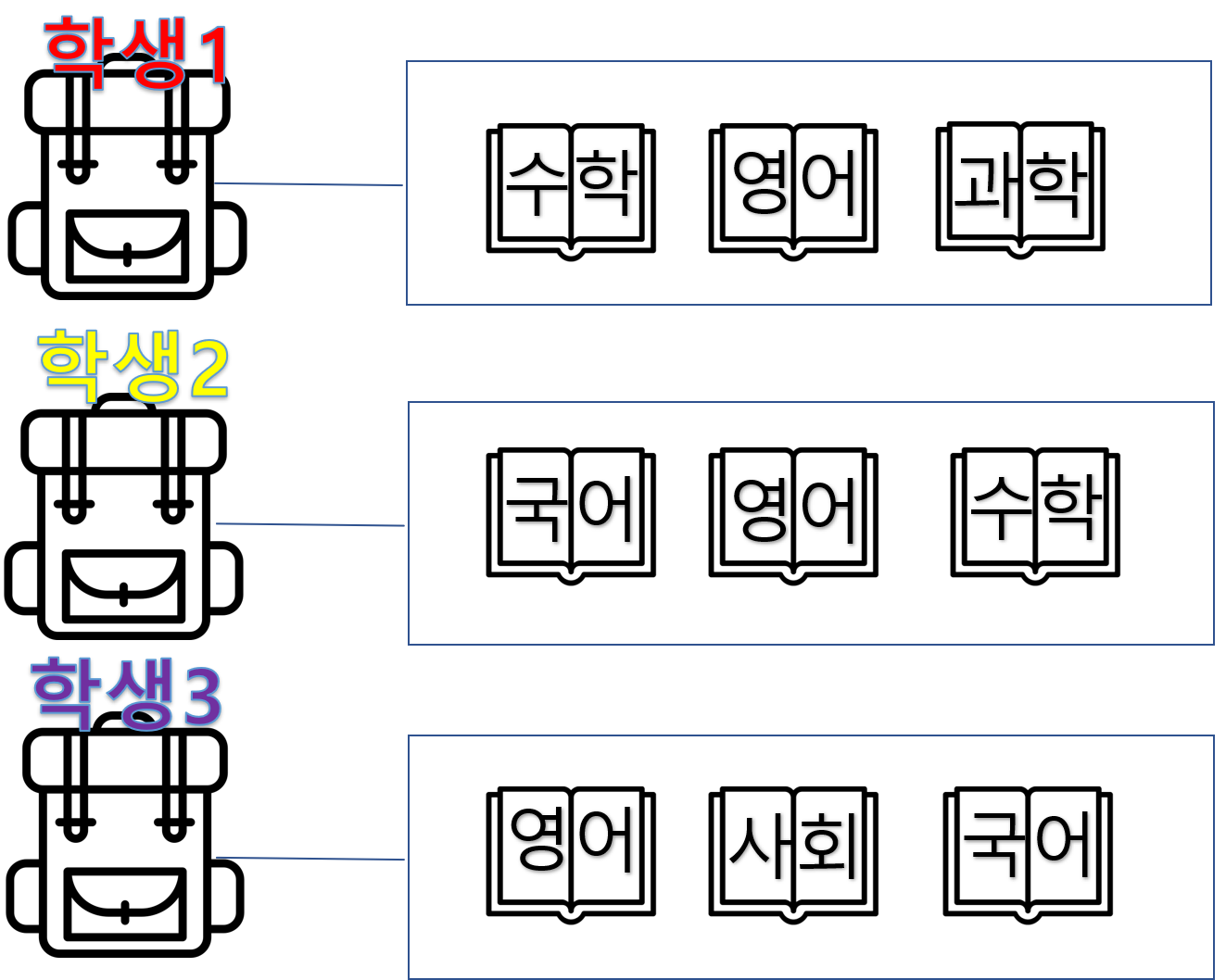
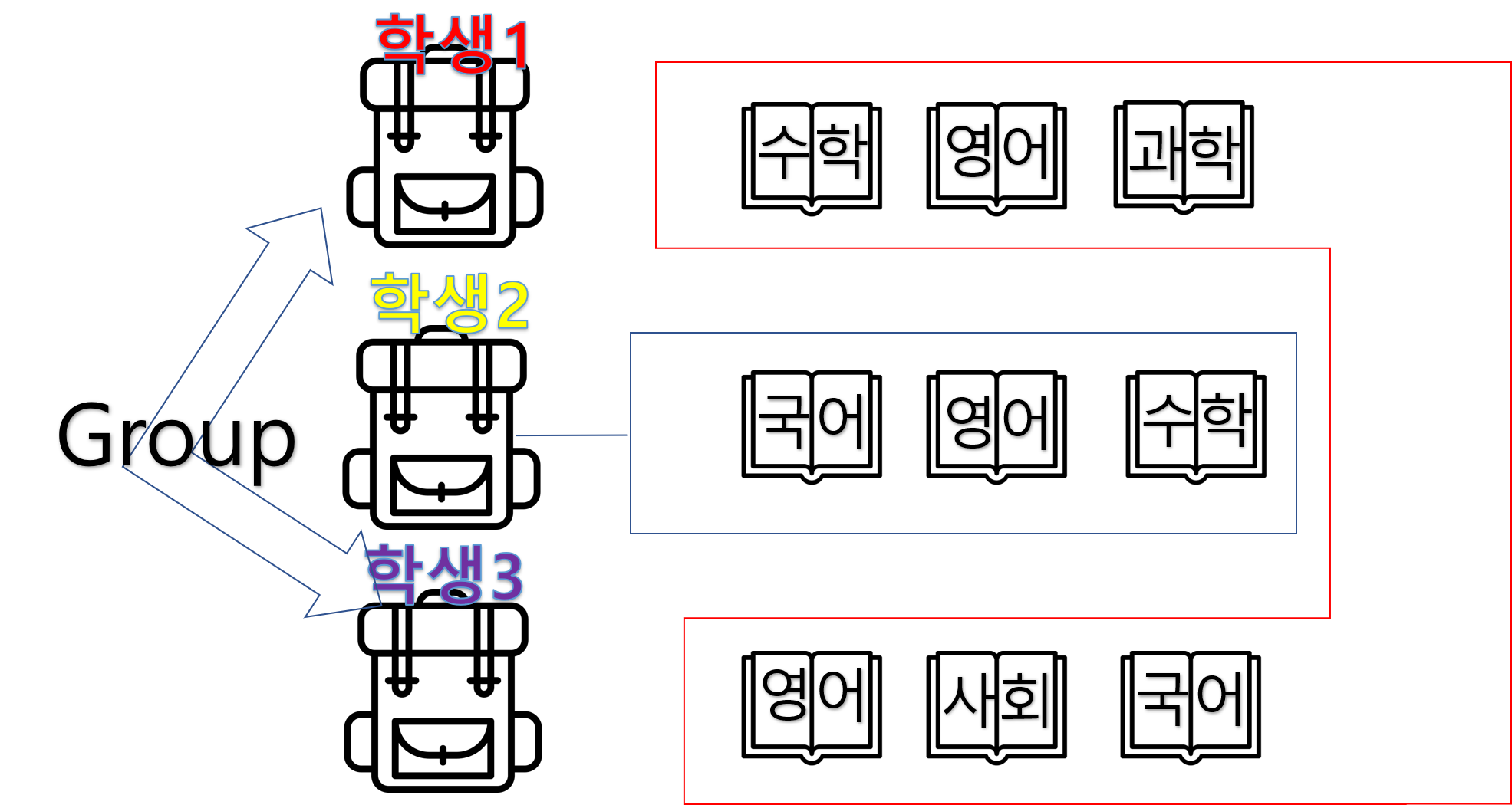
위는 학생들의 가방과 가방 안에 있는 교과서들입니다.
어떤 학생과 어떤 학생이 조를 짜야지 무조건 백점을 맞는 조가 나올 수 있을까요?
어떻게 하면 위의 답을 효율적으로 구할 수 있을까요?
주먹구구식 방법:
가장 쉬운 방법으로는 만들 수 있는 모든 조를 짜보고 조건이 맞는 지 확인하는 것입니다.
조건이 맞다는 것은 각각 만든 조가 모든 교과서를 가지고 있는 지를 확인하는 것입니다.
확인 하는 방법은 조원의 가방 안에 교과서들을 다 모아놓고 하나씩 체크하는 것입니다.
요약하면 문제 푸는 과정은 아래의 두 과정입니다.
- 랜덤하게 두 학생을 뽑아서 그룹을 만든다.
- 만든 그룹 안의 책들을 모아서 체크하고, 모든 종류의 책이 있는지 확인한다.
문제를 푸는 일련의 과정은 아래와 같습니다.
- 학생1과 학생 2과 그룹을 이루는 경우
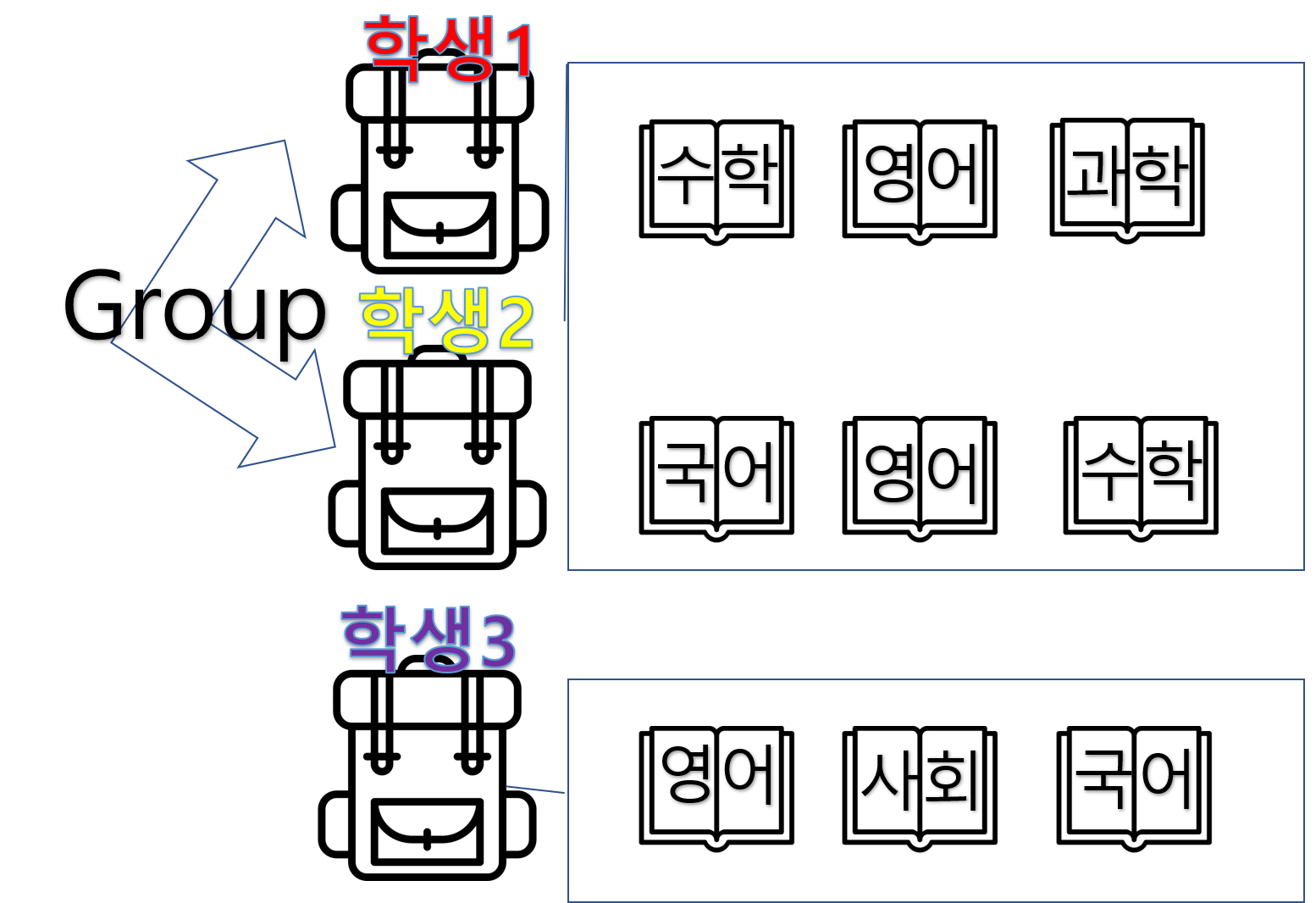
위처럼 그룹을 만들고, 만든 그룹의 책들을 모두 모아 체크하면 아래와 같습니다.
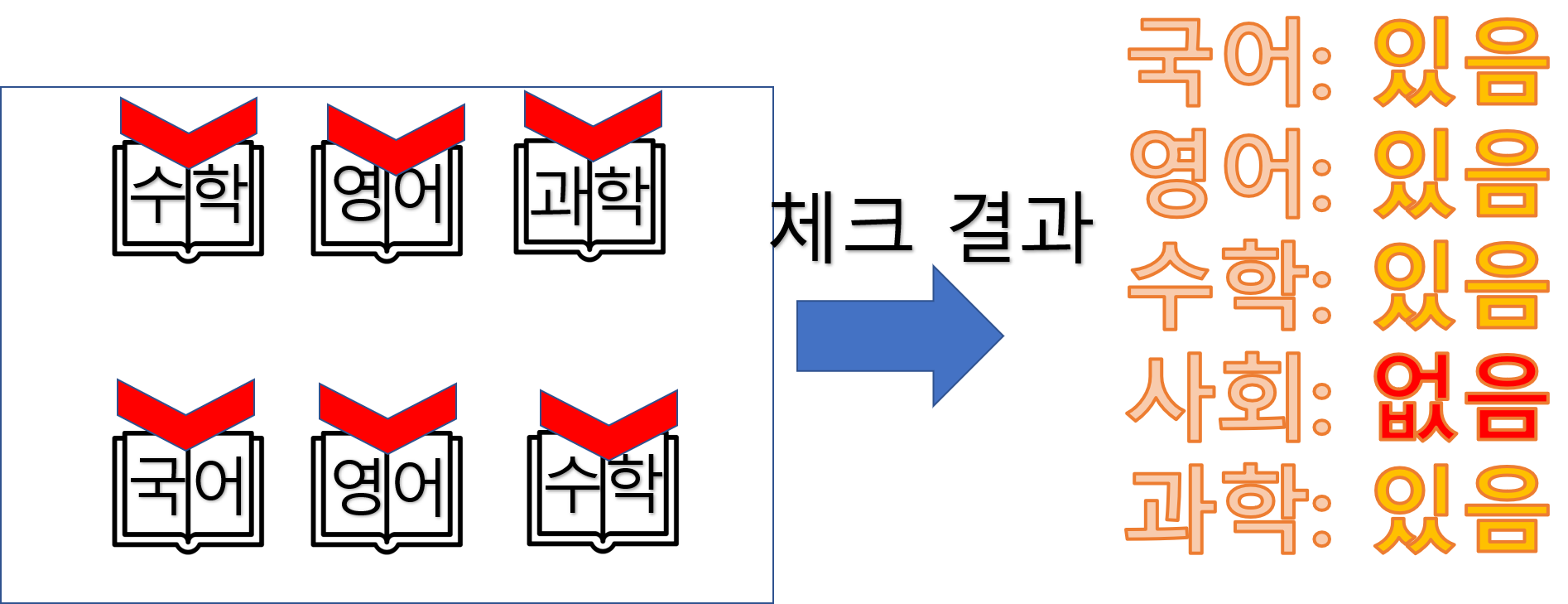
체크 결과는 사회책이 없어서 이 그룹은 백점을 맞기 힘든 그룹이라는 결과가 나옵니다.
따라서 다른 그룹을 만들고 위처럼 체크를 합니다.
- 학생2와 학생 3이 그룹을 이루는 경우
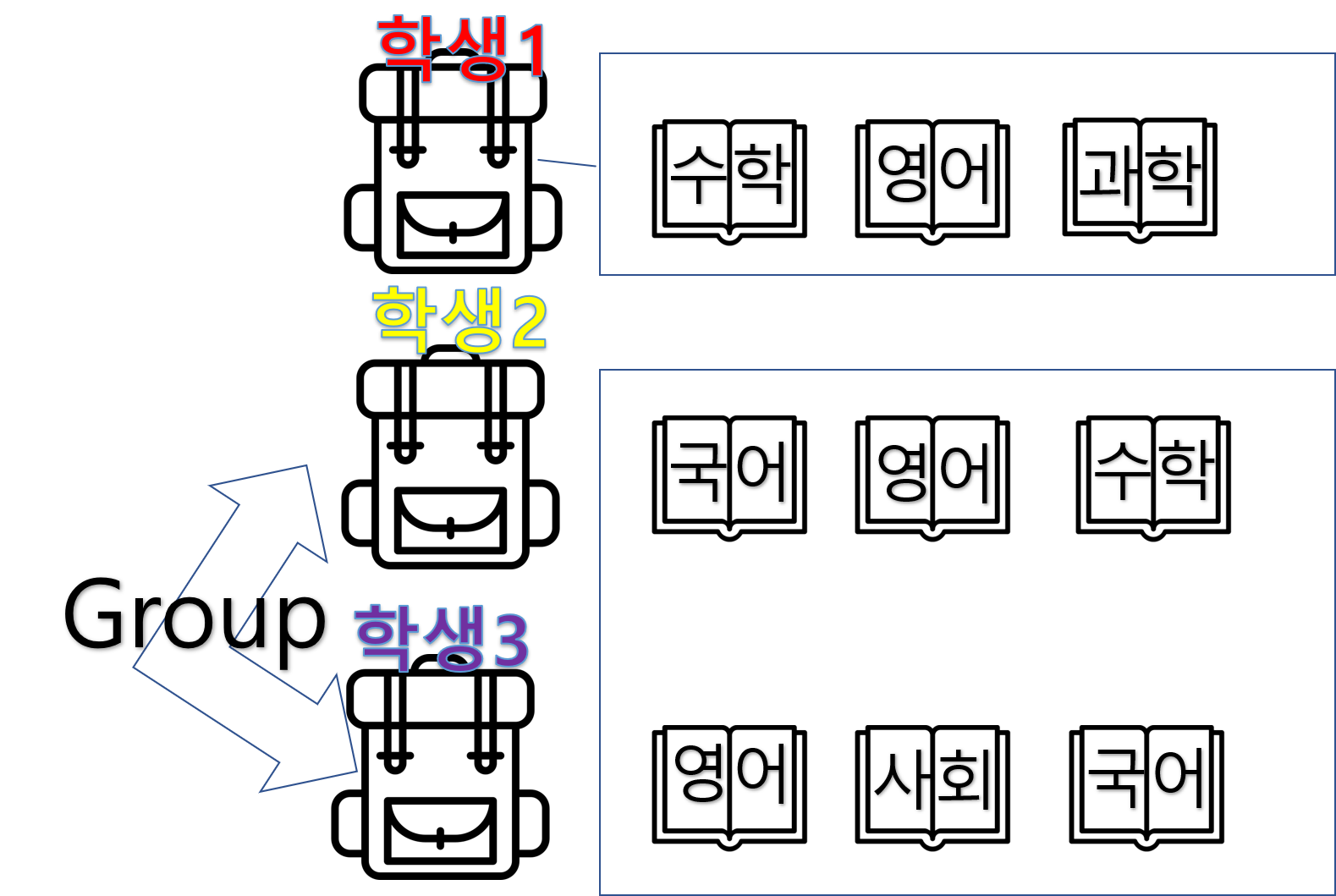
위처럼 그룹을 만들고, 만든 그룹의 책들을 모두 모아 체크하면 아래와 같습니다.
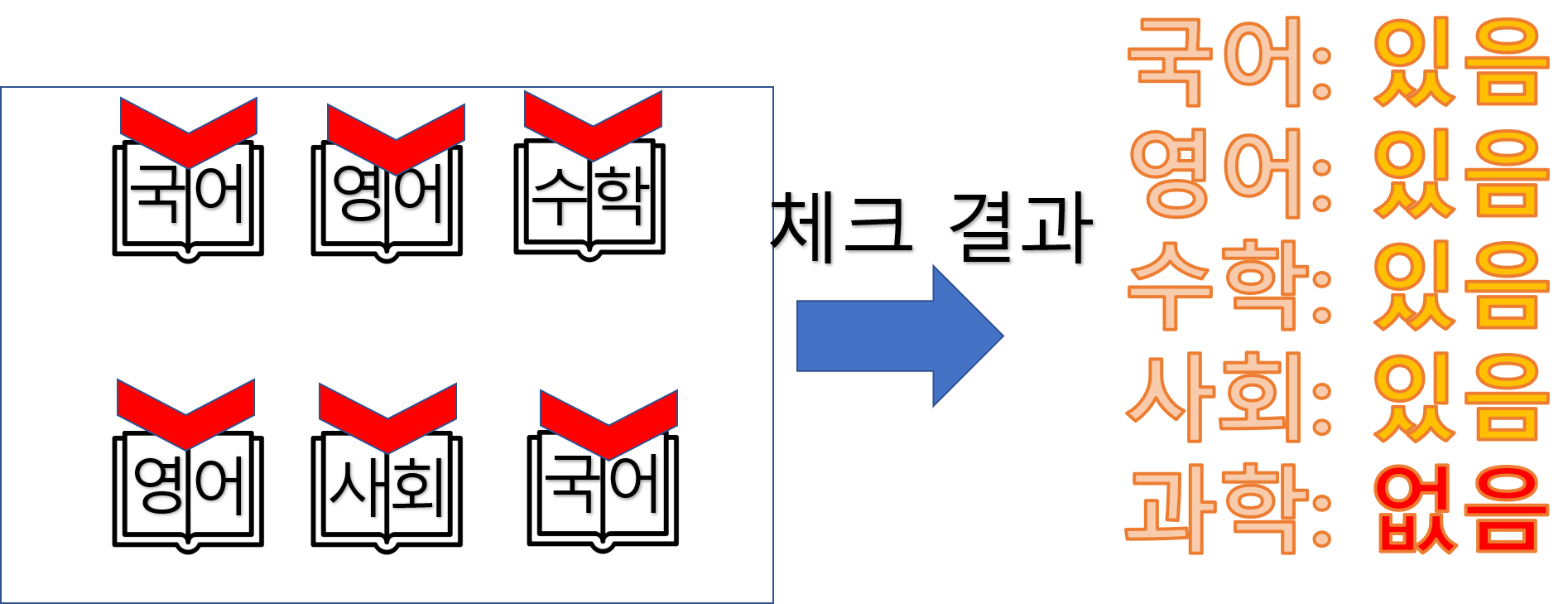
체크 결과는 과학책이 없어서 이 그룹은 백점을 맞기 힘든 그룹이라는 결과가 나옵니다.
따라서 다른 그룹을 만들고 위처럼 체크를 합니다.
- 학생1과 학생 3이 그룹을 이루는 경우
위처럼 그룹을 만들고, 만든 그룹의 책들을 모두 모아 체크하면 아래와 같습니다.
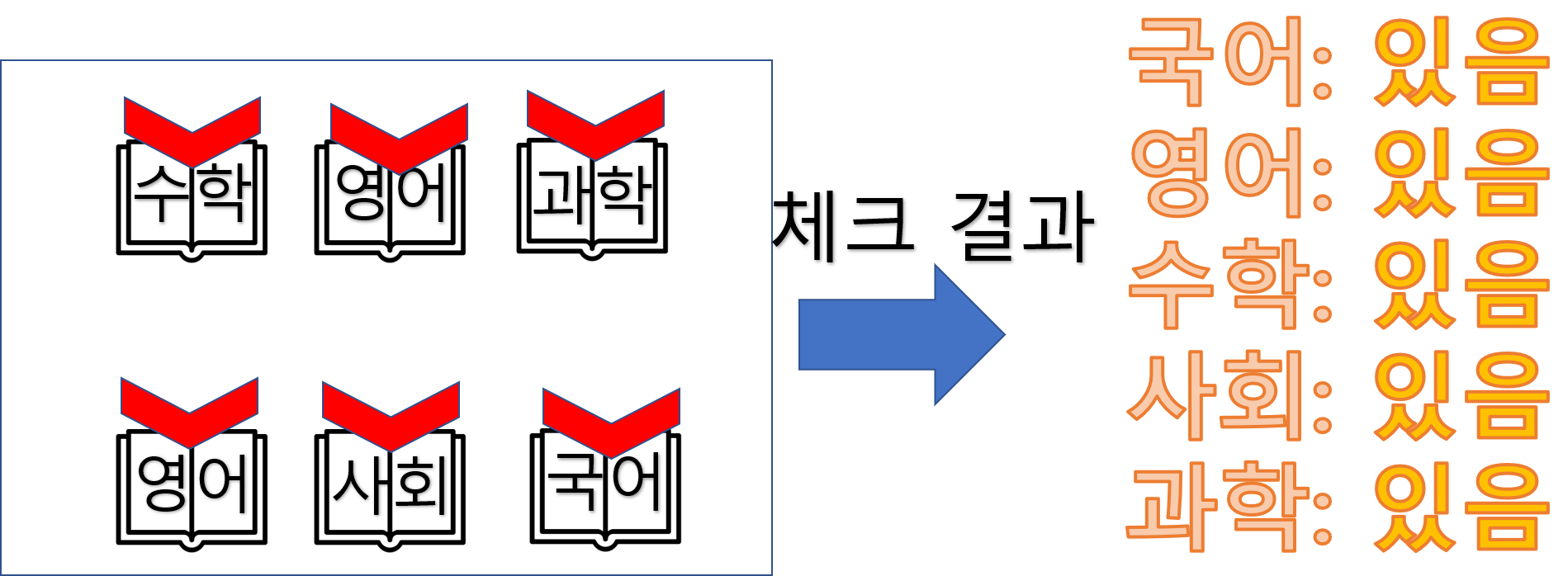
체크 결과는 모든 교과서가 있어서 백점을 맞을 수 있는 그룹이다라는 결과가 나옵니다.
따라서 그룹을 만드는 것을 멈추고 학생1-학생3 그룹이라는 답을 구할 수 있습니다.
평가:
최악의 경우, 그룹 짜는 모든 경우의 수를 고려하는 것은 피할 수 없습니다.
따라서 그룹을 만드는 시간 효율성은 O( (N*N-1)/2 )입니다.
(이 때, N = 학생의 수 이고 위 식은 N개에서 2개를 뽑는 경우와 같습니다.)
그룹을 만드는 것뿐만 아니라, 매번 그룹의 교과서를 모아서 체크도 해야 합니다.
이 경우의 수는 O(2 * M) (이 떄, M = 학생 가방 안에 있는 교과서 수)입니다.
따라서 위 값들을 곱해서 나온 전체 시간효율성은 O((N * N-1)* M)입니다.
위 두 가지 과정 중 교과서를 다 모아서 검사하는 과정은 BitMasks와
Bitwise 함수들을 이용하면 이전보다 훨씬 효율적으로 수행할 수 있습니다.
BitMask
위 문제에서 BitMask의 아이디어는 다음과 같습니다.
학생의 가방 상태를 5개의 bit로 생각하고, 각 bit는 책의 유/무를 알려주면 되지 않을까?
이 아이디어는 그림으로 표현하면 아래와 같습니다.
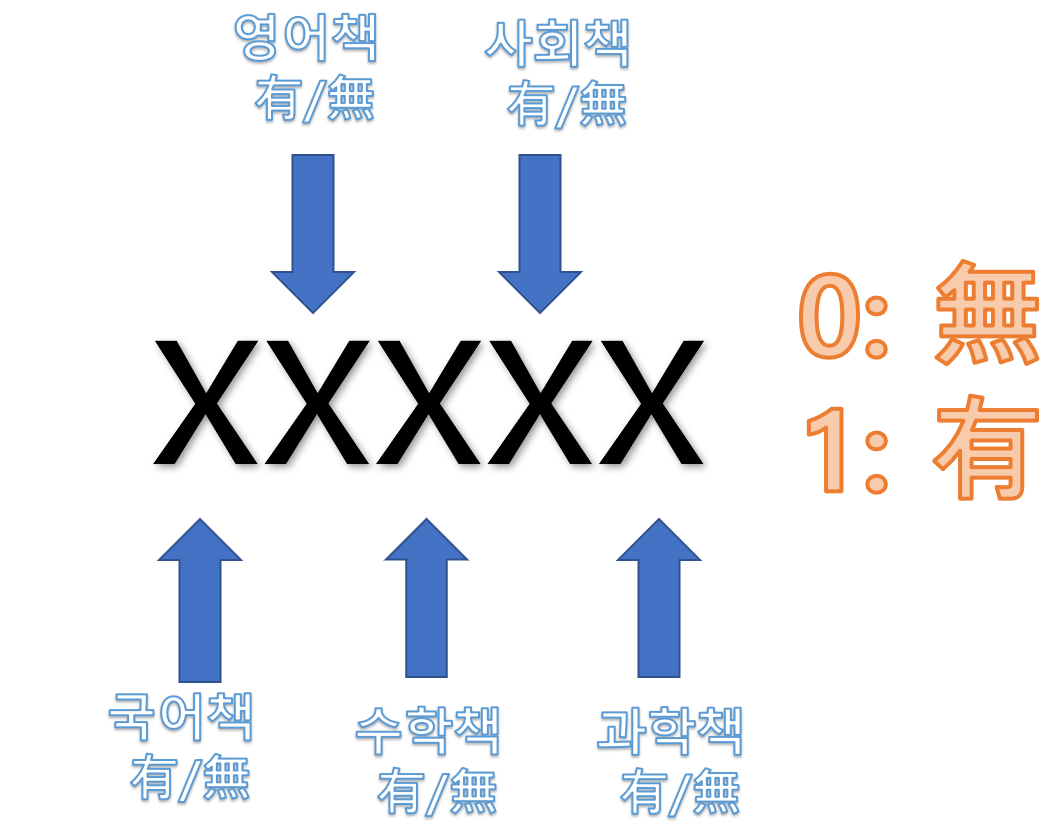
위 아이디어를 이용해서 각각 학생들의 가방의 책 상태를 표시하면 아래와 같습니다.
※ 괄호 안의 값은 십진법으로 나타낸 수 입니다.
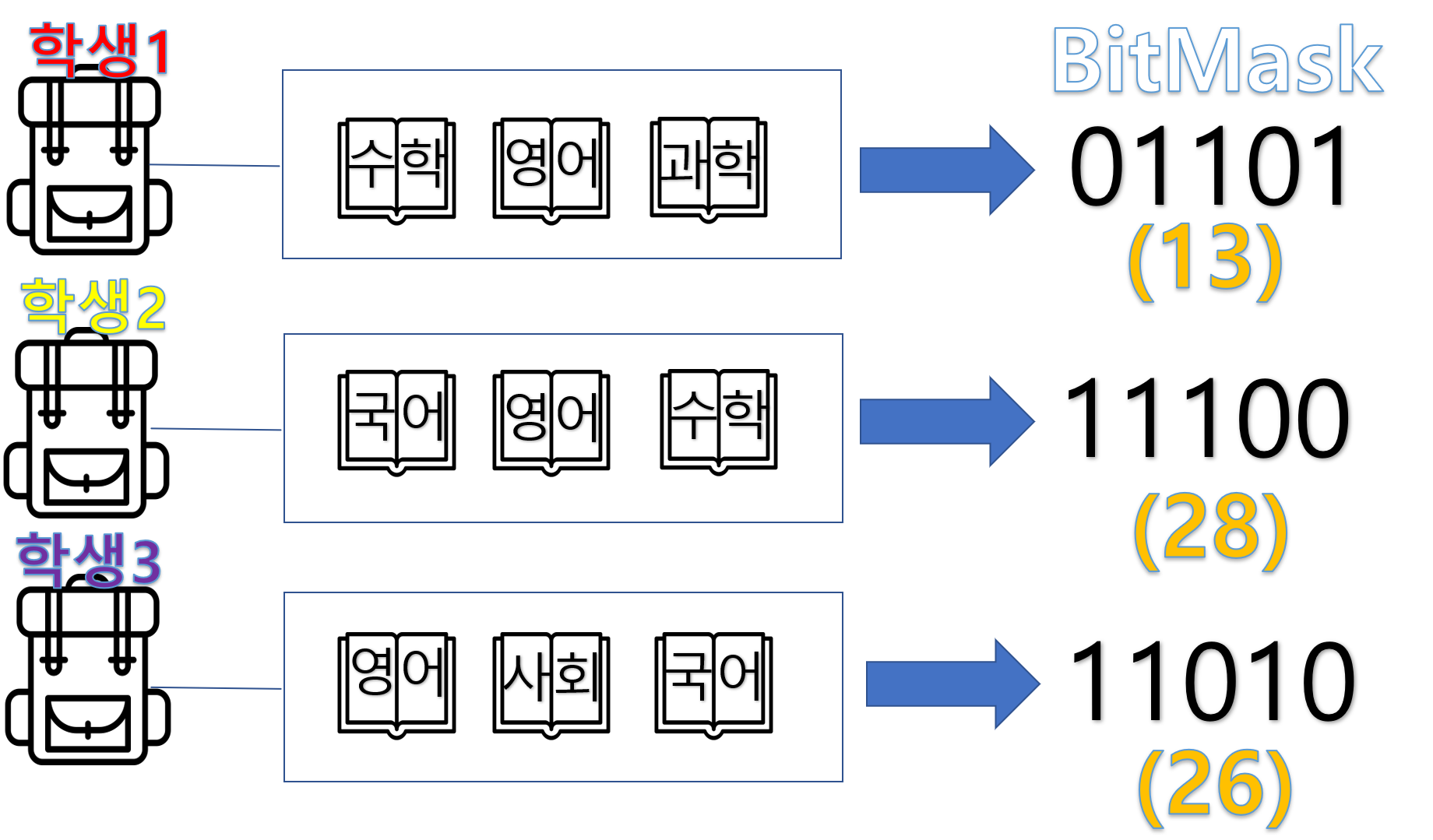
위처럼 bitmask를 이용하면 각 학생의 가방 상태를 5개의 bit로 나타낼 수 있습니다.
또한, 그룹을 만든 후의 그룹의 책의 상태는 OR을 이용하면 쉽게 구할 수 있습니다.
※ 백 점을 맞는 조는 모든 책이 있는 상태로, Bitmask로 나타내면 ‘11111’입니다.
BitMask를 이용한 풀이의 일련의 과정은 아래와 같습니다.
- 학생 1과 학생 2가 그룹을 이루는 경우
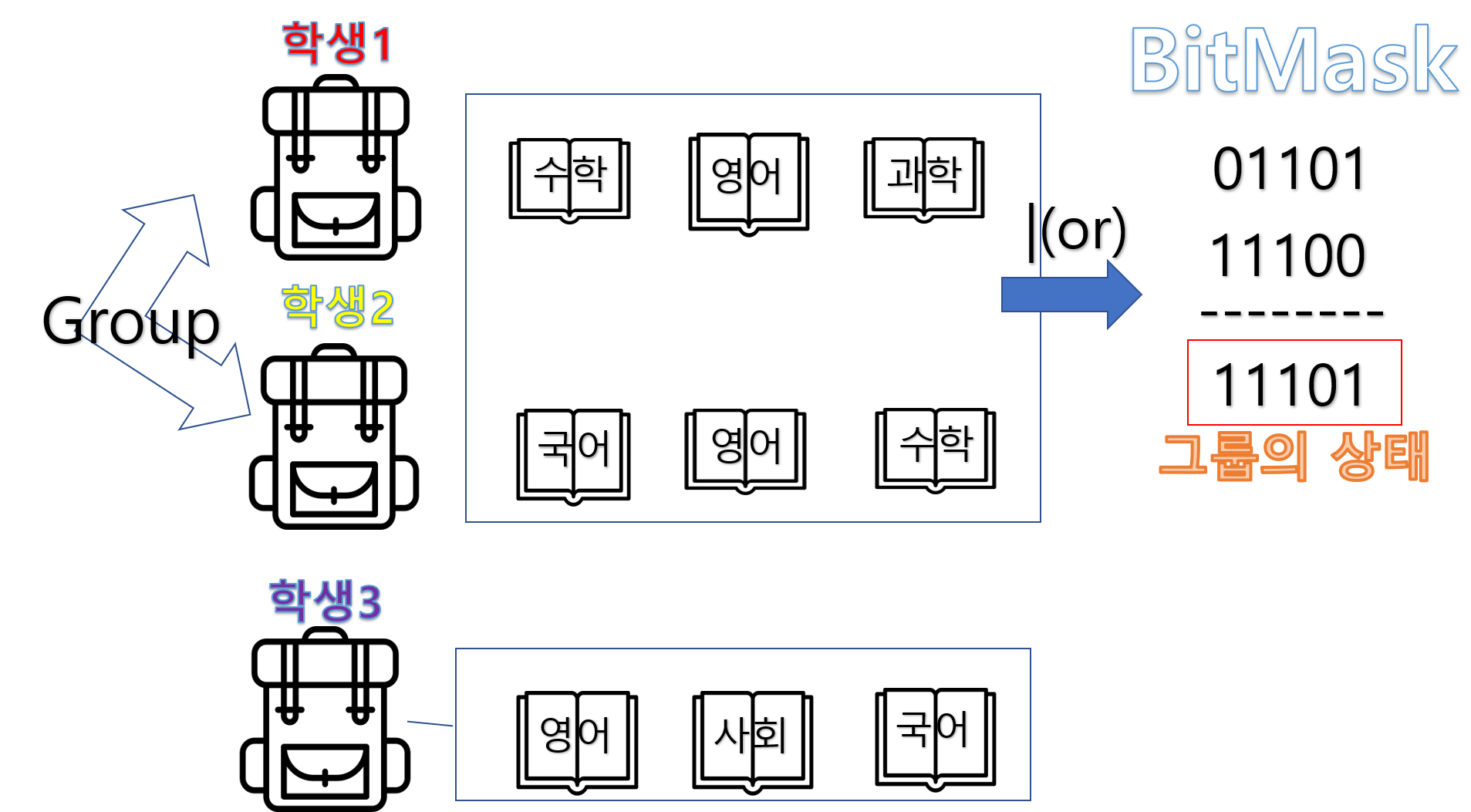
위 그룹의 책 상태는 ‘11101’으로 4번째 bit가 나타내는 사회책이 없어 답이 될 수 없습니다.
따라서 다른 그룹을 만들고 위처럼 체크를 합니다.
- 학생 2와 학생 3이 그룹을 이루는 경우
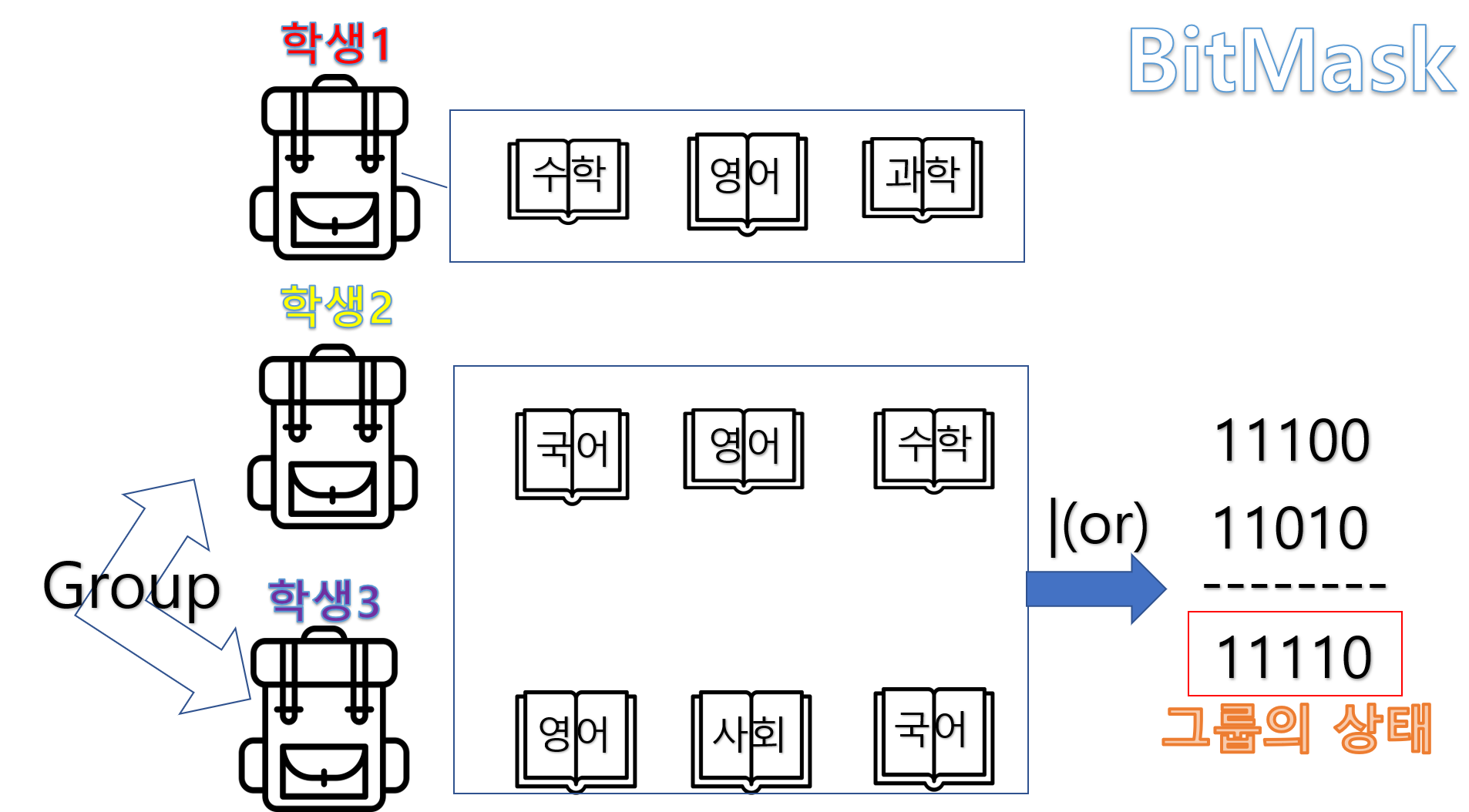
위 그룹의 책 상태는 ‘11110’으로 5번째 bit가 나타내는 과학책이 없어 답이 될 수 없습니다.
따라서 다른 그룹을 만들고 위처럼 체크를 합니다.
- 학생 1와 학생 3이 그룹을 이루는 경우
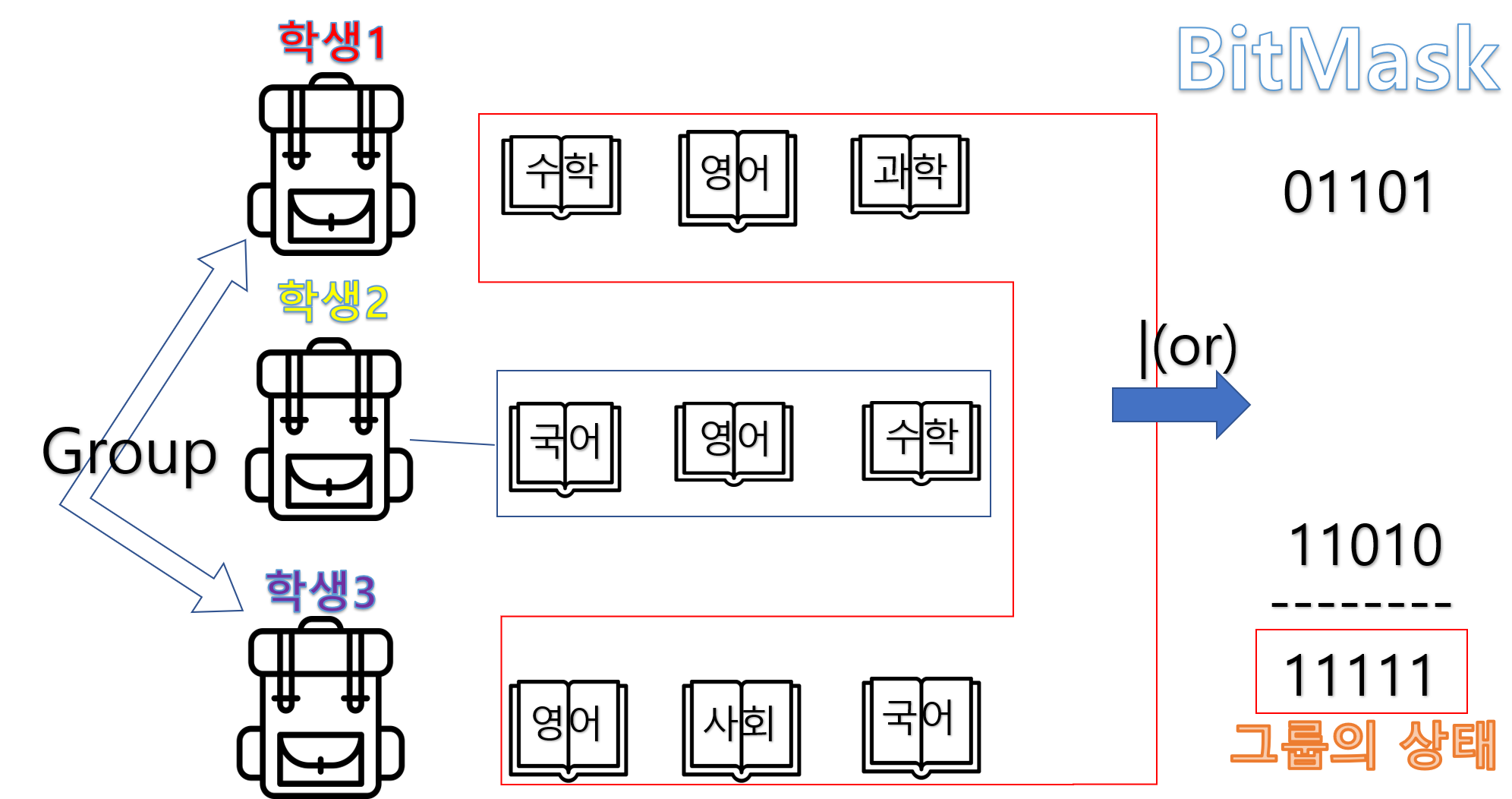
위 그룹의 책 상태는 ‘11111’, 즉 모든 책이 있는 상태이고 따라서 우리가 찾는 답입니다.
따라서 다른 그룹을 만드는 걸 멈추고 답을 도출합니다.
BitMask 평가:
처음의 주먹구구식 방법과는 다르게 data-preprocessing 시간이 걸립니다.
이유는 기존의 list 형태로 받은 책들을 가방의 bitMask로 바꿔야 하기 때문이죠.
하지만 그 후에 그룹의 상태를 얻을 때는 이전에 O(2 * M)의 시간이 걸렸던 것과
다르게, O(1)로 가능합니다. Or operater을 사용해서 모든 책 유무를 한 번에
비교하고 그룹의 상태를 얻는 것이 가능하기 때문입니다.
전체 시간효율성은 모든 그룹을 만드는 경우인 O((N * N-1)/ 2)입니다.
한계점:
이 문제처럼 유/무 처럼 0과 1로만 상태 표현이 가능하면 BitMask가 효과적입니다.
그러나 만약 ‘책은 있지만 반이 찢어진 상태’, ‘책은 있지만 1/4만 있는 상태’처럼
0과 1로 책의 상태를 설명하지 못하는 경우가 있다면, 조금 복잡해 집니다.
이를 해결하기 위해 n개의 bit를 하나로 묶어 책 상태를 표현할 수 있습니다.
하지만, 고려 해야할 상태가 많은 경우에는 이 과정에서 비효율성이 일어날 수 있습니다.
구현 by Python
import os
import sys
def makeBitMask(student): # Bitmask 만들기
bitmask = 0
if '국어' in student: bitmask |= (1<<4)
if '영어' in student: bitmask |= (1<<3)
if '수학' in student: bitmask |= (1<<2)
if '사회' in student: bitmask |= (1<<1)
if '과학' in student: bitmask |= (1<<0)
return bitmask
def solve(student_list): # 문제 풀이
bitmask_list = []
for student in student_list: bitmask_list.append(makeBitMask(student)) #data-PreProcessing
for i in range(len(bitmask_list)): #그룹 만들고 비교
for j in range(i+1, len(bitmask_list)):
if bitmask_list[i]|bitmask_list[j] == (1<<5) - 1:
return (i, j) # 답 도출
